Les Convertisseurs Analogiques Numériques (CAN)
Nous utilisons le même schéma que dans le paragraphe précédent. Nous présentons d'abord un schéma de principe simple voire naïf pour bien s'approprier le principe du fonctionnement du convertisseur analogique numérique puis nous montrons des variantes qui complexifient les circuits mais qui permettent de résoudre des problèmes que présentent les circuits les plus simples et enfin, nous terminons par une étude des performances des CAN et CNA pour une utilisation professionnelle.
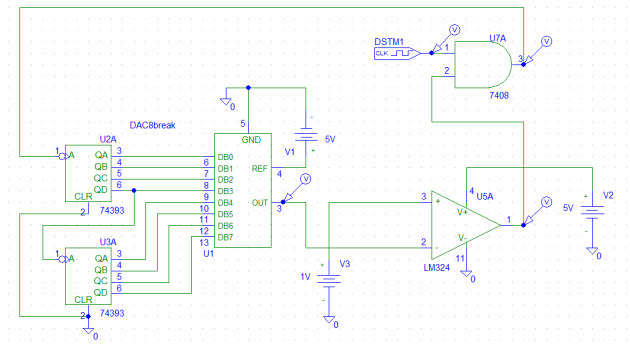
Nous commençons par un circuit naïf qui exploite un CNA représenté ci-dessous :
Le principe de fonctionnement est le suivant : la tension analogique à convertir entre sur un comparateur qui peut être un simple ampli-op alimenté en disymétrique et qui fonctionne en régime saturé. Le cycle de conversion commence par la remise à 0 du compteur qui entre sur le CNA. La tension de sortie du CNA est donc initialement nulle, au début du cycle de conversion. Comme cette tension de sortie du CNA entre sur la seconde entrée du comparateur et si la tension à convertir est positive, la sortie du comparateur est à 1. L'horloge traverse donc la porte ET et arrive sur le compteur qui compte. La sortie du CNA élabore donc une tension en rampe qui croît à chaque coup d'horloge jusqu'à ce que la sortie du CNA devienne supérieure à la tension à convertir. A ce moment, le comparateur bascule à 0 et l'horloge ne passe plus la porte ET, le compteur ne reçoit plus de front actif, il s'est figé sur un nombre qui représente l'équivalent binaire de la tension analogique à convertir.
Le lien ci-dessous permet de télécharger le schéma PSpice du CAN à rampe numérique.
Ce convertisseur dit à rampe numérique, possède toutefois quelques inconvénients : en premier lieu, le temps de conversion est lent et dépend de la valeur à convertir. Il est court pour les faibles valeurs de tension mais long, très long pour les valeurs élevées. Ce défaut est assez rédhibitoire et le convertisseur à rampe numérique est juste intéressant pour présenter la fonction de conversion analogique numérique mais jamais utilisé dans la pratique. Il revient à comparer la tension à convertir à tous les niveaux de quantification possibles, l'un après l'autre, du plus petit au plus grand. C'est comme si on vous demandait de deviner la somme d'argent qu'on vous offrira si vous y parvenez dans un temps donné. Supposons que vous devez deviner une somme comprise entre 0 et 4095 (ça correspond à 12 bits). Allez-vous proposer la suite suivante :
- (vous) 0 € ?
- (l'animateur) plus !
- (vous) 1 € ?
- (l'animateur) plus !
- (vous) 2 € ?
- (l'animateur) plus !
- (vous) 3 € ?
- (l'animateur) plus !
- (vous) 4 € ?
- (l'animateur) plus !
- (vous) 5 € ?
- (l'animateur) plus !
- (vous) 6 € ?
et ainsi de suite ?
Bien sûr que non ! On montre (au sens mathématique) que la méthode pour converger le plus vite possible vers la somme à deviner consiste à appliquer la dichotomie, c'est à dire, la séparation en deux de l'intervalle dans lequel on cherche la valeur inconnue. Pour illustrer le principe du convertisseur à approximation successive qui utilise ce principe de dichotomie, nous traitons un cas particulier avec comme plus haut, la valeur 2014 sur un nombre de 12 bits donc compris entre 0 et 4095. Le premier essai correspond au milieu de l'intervalle total et nous écrivons la totalité des essais avec la réponse de l'animateur comme plus haut :
- (vous) 2047 ?
- (l'animateur) moins ! (il faut deviner 2014). On sait à présent qu'on doit chercher entre 0 et 2047. On coupe l'intervalle en deux (dichotomie)
- (vous) 1023 ?
- (l'animateur) plus ! Il faut désormais chercher entre 1024 et 2047, on coupe cet intervalle en deux.
- (vous) 1535 ?
- (l'animateur) plus !
- (vous) 1791 ?
- (l'animateur) plus !
- (vous) 1919 ?
- (l'animateur) plus !
- (vous) 1983 ?
- (l'animateur) plus !
- (vous) 2015 ?
- (l'animateur) moins !
- (vous) 1999 ?
- (l'animateur) plus !
- (vous) 2007 ?
- (l'animateur) plus !
- (vous) 2011 ?
- (l'animateur) plus !
- (vous) 2013 ?
- (l'animateur) plus !
- (vous) 2014 !
- (l'animateur) Yes !!!!
On rappelle que 
codé sur 12 bits. Vous observerez qu'on obtient le nombre en représentation binaire en convertissant les réponses « moins » et « plus » de l'animateur de la première (chronologiquement) à la dernière en considérant la première comme le bit de poids fort dans le nombre recherché. Par ailleurs, combien d'essais ont été nécessaires ? 12 ! Si vous pensez que la valeur numérique 2014 à deviner conduit à 12 par hasard, qui est le nombre de bits nécessaire pour représenter les nombres de l'intervalle dans lequel on cherche la valeur inconnue, je vous propose de refaire l'algorithme ci-dessus pour une autre valeur quelconque entre 0 et 4095. Vous serez sans doute un peu surpris de constater qu'il faut toujours 12 essais (sauf dans les cas rares où le nombre à deviner correspond à une valeur de dichotomie). Néanmoins, si l'animateur répond toujours par plus ou moins au sens de supérieur ou égal ou inférieur ou égal, sans vous dire avant les 12 essais, si vous êtes tombés par extraordinaire sur la valeur inconnue qui correspond à un des seuils de dichotomie, vous êtes néanmoins certain d'encadrer la valeur inconnu en 12 essais.
C'est le principe du convertisseur à approximations successives. Hélas sa structure logique ne peut pas être simplement simulée sous PSpice. On se contentera d'un schéma de principe sans plus d'explication.
