Nathalie Van de Wiele - Sup PCSI - 2001
nvdw@ac-nice.fr

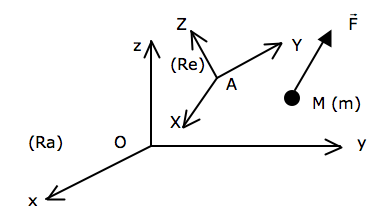
Les référentiels non galiléens

1. Le principe fondamental de la dynamique dans un référentiel non galiléen - Les forces d’inertie
2. Eléments de dynamique terrestre
- 2.1. Principe fondamental de la dynamique appliqué au point M de masse m dans le référentiel terrestre, non galiléen
  - 2.1.1. Expression de $\vec{a_{T}} (M)$ , accélération dans le référentiel terrestre, en fonction de $\vec{a_{C_{0}}} (M)$ , accélération dans le référentiel de Copernic
  - 2.1.2. Appliquons le principe fondamental de la dynamique dans le référentiel de Copernic galiléen
- 2.2. Interprétation
3. Etude du champ de pesanteur
- 3.1. Etude du champ des marées
- 3.2. Etude du terme centrifuge : la direction de la verticale
4. Influence du terme de Coriolis
5. Impesanteur

1. Le principe fondamental de la dynamique dans un référentiel non galiléen - Les forces d’inertie

(Ra) est un référentiel absolu lié au solide de référence (Oxyz), supposé galiléen.

(Re) est un référentiel d’entraînement lié au solide de référence (AXYZ), en mouvement quelconque, de vecteur instantané de rotation $\vec{Ω}$ , par rapport à (Ra), a priori non galiléen.

M est un point matériel de masse m soumis à la force $\vec{F}$ .

Référentiels

Avec les notations usuelles, le principe fondamental de la dynamique dans (Ra) galiléen : $m \vec{a_{a}} (M) = \vec{F}$ , et la loi de composition des accélérations : $\vec{a_{r}} (M) = \vec{a_{a}} (M) - \vec{a_{e}} (M) - \vec{a_{c}} (M)$ , donnent : $m \vec{a_{r}} (M) = \vec{F} - m \vec{a_{e}} (M) - m \vec{a_{e}} (M)$ , c'est le

principe fondamental de la dynamique dans un référentiel (Re) non galiléen : $m \vec{a_{r}} (M) = \vec{F} + \vec{F_{ie}} + \vec{F_{ic}}$

$\vec{F_{ie}} = - m \vec{a_{e}} (M)$ est la force d'inertie d'entraînement ( $\vec{a_{e}} (M)$ se calcule à l'aide de la notion de point coïncidant).
$\vec{F_{ic}} = - m \vec{a_{c}} (M) = - 2 m \vec{Ω} \land \vec{V_{r}} (M)$ est la force d'inertie de Coriolis. Elle est nulle dans le cas particulier d’un entraînement de translation ( $\vec{Ω} = \vec{0}$ ), ou à l'équilibre dans (Re) ( $\vec{V_{r}} (M) = \vec{0}$ ).

Mais les forces d’inertie ne sont pas « véritables » au sens où elles disparaissent si on traite le problème par application du principe fondamental de la dynamique dans (Ra) , ce qui est une autre façon de le résoudre. A ce titre, la force $\vec{F}$ est dite « force véritable ».

1. Précisons la notion de force d'inertie d'entraînement dans le cas d'un pendule à l'équilibre dans un véhicule entraîné par rapport au référentiel terrestre (galiléen avec une excellente approximation pour cette expérience), la force d'inertie de Coriolis étant nulle à l'équilibre relatif.

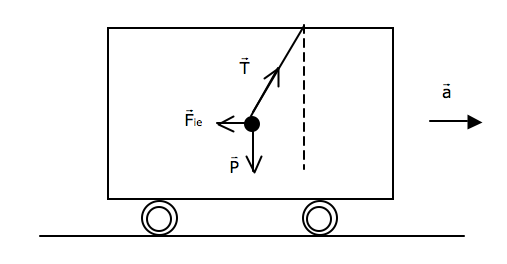
a) Cas d’un entraînement de translation d'accélération $\vec{a}$ : $\vec{F_{ie}} = - m \vec{a_{e}} (M) = - m \vec{a}$ .

C’est le cas où la voiture accélère en ligne droite sur une route horizontale. Pour une accélération constante l’équilibre relatif du pendule s’écrit : $\vec{0} = \vec{P} + \vec{T} + \vec{F_{ie}}$ .

Entraînement de translation

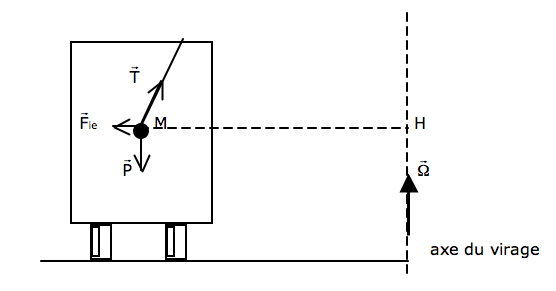
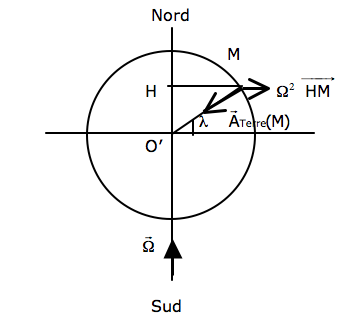
b) Cas d’un entraînement de rotation uniforme autour d’un axe fixe de vecteur $\vec{Ω}$ : $\vec{F_{ie}} = - m \vec{a_{e}} (M) = m Ω^{2} \vec{HM}$ , H étant le projeté de M sur l'axe de rotation, la force d'inertie est centrifuge.

C’est le cas où la voiture aborde un virage à vitesse constante sur une route horizontale. L’équilibre relatif du pendule s’écrit : $\vec{0} = \vec{P} + \vec{T} + \vec{F_{ie}}$ .

Entraînement de rotation

2. Précisons la notion de force d'inertie de Coriolis en faisant référence à lexpérience historique du pendule de Foucault menée en 1851 au Panthéon, destinée à mettre en évidence la rotation de a Terre autour de l'axe des pôles. A l’aide d’un pendule de longueur L = 67 m , Foucault observe une rotation du plan d’oscillation du pendule à raison d’un tour en 31 h 29 min .

2. Eléments de dynamique terrestre

Référentiel terrestre

Rappelons que :

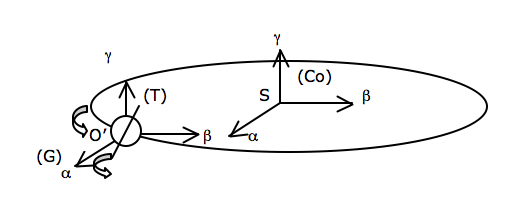
(Co) est le référentiel de Copernic, c'est le meilleur référentiel galiléen identifiable expérimentalement ;

(G) est le référentiel géocentrique, en translation elliptique quasi circulaire par rapport à (Co) , donc non rigoureusement galiléen ;

(T) est le référentiel terrestre, en rotation par rapport à (T) , donc non rigoureusement galiléen, défini ci-après.

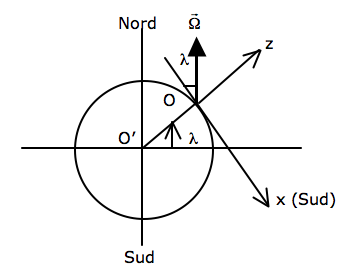
O’ étant le centre de masse de la Terre, le référentiel terrestre en un lieu O de latitude λ est tel que : $\vec{OO'}$ définit $\vec{u_{z}}$ , Ox est l'horizontale vers le Sud, Oy est l'horizontale vers l'Est.

La rotation de la Terre autour de l’axe des pôles est une rotation uniforme de vecteur $\vec{Ω}$ ,

de direction constante dans le temps (en négligeant le fait que l’axe des pôles décrit un cône en 26000 ans, c’est à dire la précession des équinoxes),
de valeur $Ω = \frac{2 π}{T}$ où T est la durée du jour sidéral, c'est à dire la période de rotation de la Terre sur elle-même (T = 23 h 56 min 4 s ).

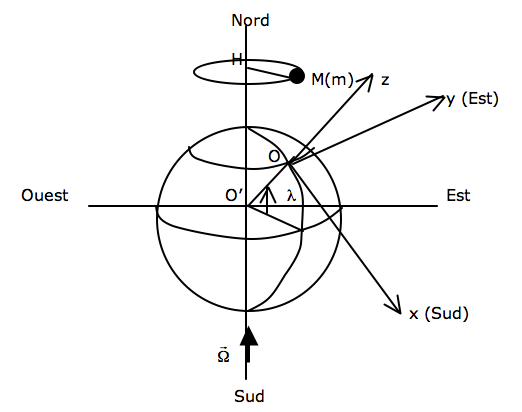
Accélération d'entraînement

Dans l’entraînement du référentiel terrestre par rapport au référentiel géocentrique, l’accélération d’entraînement du point M est $\vec{a_{e}} (M) = - Ω^{2} \vec{HM}$ .

2.1. Principe fondamental de la dynamique appliqué au point M de masse m dans le référentiel terrestre, non galiléen

En reprenant la démarche précédente (composition des accélérations et principe fondamental de la dynamique dans le référentiel de Copernic, galiléen) nous verrons apparaître les termes d’inertie d’entraînement et de Coriolis.

2.1.1. Expression de $\vec{a_{T}} (M)$ , accélération dans le référentiel terrestre, en fonction de $\vec{a_{C_{0}}} (M)$ , accélération dans le référentiel de Copernic

Il faut d’abord passer du référentiel de Copernic (Co) (absolu) au référentiel géocentrique (G) (d’entraînement) :

$\vec{a_{G}} (M) = \vec{a_{C_{0}}} (M) - \vec{a_{e}} (M) - \vec{a_{c}} (M)$ .

Avec $\vec{a_{e}} (M) = \vec{a_{C_{0}}} (O')$ (notion de point coïncidant, avec (G) en translation par rapport à (C₀)), et $\vec{a_{c}} (M) = \vec{0}$ ((G) étant en translation par rapport à (C₀)), on a :

$\vec{a_{G}} (M) = \vec{a_{C_{0}}} (M) - \vec{a_{C_{0}}} (O')$ (1)
Il faut ensuite passer du référentiel géocentrique (absolu) au référentiel terrestre (T) (d’entraînement) :
$\vec{a_{T}} (M) = \vec{a_{G}} (M) - \vec{a_{e}} (M) - \vec{a_{c}} (M)$ .

Avec $\vec{a_{e}} (M) = - Ω^{2} \vec{HM}$ et $\vec{a_{c}} (M) = 2 \vec{Ω} \land \vec{v_{T}} (M)$ , on a :

$\vec{a_{T}} (M) = \vec{a_{G}} (M) + Ω^{2} \vec{HM} - 2 \vec{Ω} \land \vec{v_{T}} (M)$ (2)
(1) et (2) donnent :
$\vec{a_{T}} (M) = \vec{a_{C_{0}}} (M) - \vec{a_{C_{0}}} (O') + Ω^{2} \vec{HM} - 2 \vec{Ω} \land \vec{v_{T}} (M)$ (3)

2.1.2. Appliquons le principe fondamental de la dynamique dans le référentiel de Copernic galiléen

D’abord à la Terre, supposée ponctuelle en O’ , de masse $M_{Terre}$ , soumise au champ gravitationnel créé par le Soleil et les autres astres,noté $\vec{A_{astres}}$ : $M_{Terre} \vec{a_{C_{0}}} (O') = M_{Terre} \vec{A_{astres}} (O')$ =>
$\vec{a_{C_{0}}} (O') = \vec{A_{astres}} (O')$ (4)
Ensuite au point M de masse m , soumis au champ gravitationnel créé par la Terre, noté $\vec{A_{Terre}}$ , au champ gravitationnel créé par le Soleil et les autres astres et à une éventuelle force appliquée $\vec{F_{appl}}$ : => $m \vec{a_{C_{0}}} (M) = m \vec{A_{Terre}} (M) + m \vec{A_{astres}} (M) + F_{appl}$ =>
$\vec{a_{C_{0}}} (M) = \vec{A_{Terre}} (M) + \vec{A_{astres}} (M) + \frac{\vec{F_{appl}}}{m}$ (5)
Finalement, (3) compte tenu de (4) et (5) donne :
$\vec{a_{T}} (M) = \vec{A_{Terre}} (M) + \vec{A_{astres}} (M) - \vec{A_{astres}} (O') + Ω^{2} \vec{HM} + 2 \vec{Ω} \land \vec{v_{T}} (M) + \frac{\vec{F_{appl}}}{m}$ (6)

2.2. Interprétation

Par multiplication par m nous obtenons :

$m \vec{a_{T}} (M) = m (\vec{A_{Terre}} (M) + \vec{A_{astres}} (M) - \vec{A_{astres}} (O') + Ω^{2} \vec{HM}) - 2 m \vec{Ω} \land \vec{v_{T}} (M) + \vec{F_{appl}}$

Le champ de pesanteur en M est :

$\vec{g} (M) = \vec{A_{Terre}} (M) + \vec{A_{astres}} (M) - \vec{A_{astres}} (O') + Ω^{2} \vec{HM}$

Il contient :

le terme principal $\vec{A_{Terre}} (M)$ ;
le terme différentiel du champ $\vec{A_{astres}}$ , appelé champ des marées : $\vec{C} (M) = \vec{A_{astres}} (M) - \vec{A_{astres}} (O')$ , négligeable dans la plupart des applications sauf précisément dans le cas des marées où les masses d'eau concernées sont considérables ;
le terme centrifuge $Ω^{2} \vec{HM}$ .

Le poids est défini par , sa direction définit la verticale du lieu.

Le principe fondamental de la dynamique appliqué à M dans le référentiel terrestre non galiléen s’écrit :
$m \vec{a_{T}} (M) = m \vec{g} (M) + \vec{F_{ic}} + \vec{F_{ie}}$ (7)

Le terme d’entraînement est dans le champ de pesanteur, la force d’inertie de Coriolis est : $\vec{F_{ic}} = - 2 m \vec{Ω} \land \vec{v_{T}} (M)$ .

3. Etude du champ de pesanteur

3.1. Etude du champ des marées

Plaçons-nous dans le cas simple où un seul astre considéré comme ponctuel, en B , de masse $M_{astre}$ , agit sur la Terre.

La terre est supposée parfaitement sphérique, de rayon $R_{Terre}$ , de centre O', avec O'B = d .

L’expression du champ $\vec{A_{astre}} (M)$ = $\frac{G M_{astre}}{{(MB)}^{2}} \vec{u_{MB}}$ (G constante de gravitation universelle, $\vec{u_{MB}}$ vecteur unitaire de M vers B ), appliquée successivement enO', $M_{1}$ et $M_{2}$ (on effectue un développement limité en $R_{Terre} / d < < 1$ ) :

$\vec{C} (M_{1}) = - \vec{C} (M_{1}) = 2 G R_{Terre} \frac{M_{astre}}{d^{3}} \vec{u_{z}}$ ( $\vec{u_{z}}$ unitaire : voir la figure).

Pour un modèle grossier de Terre-océan, on a deux marées, « sous » l’astre (voir la figure 2).

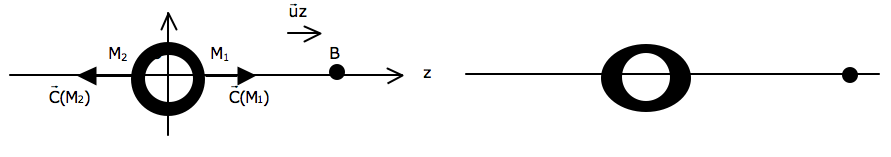
Marées

figure 1 figure 2

On calcule : $\frac{\frac{M_{Soleil}}{{(d_{Terre - Soleil})}^{3}}}{\frac{M_{Lune}}{{(d_{Terre - Lune})}^{3}}} = 0,45$ : l'action de la Lune est prépondérante, mais l'action du Soleil n'est pas négligeable.

La Lune et le Soleil conjuguent leurs effets avec 4 situations remarquables :

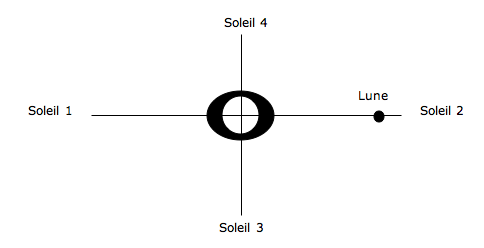
Action du soleil et de la lune

Le plan de l’orbite lunaire étant incliné de 5° sur le plan de l’écliptique, les phases de la Lune correspondant à la position du Soleil sont respectivement :
Soleil 1 : pleine Lune ; Soleil 2 : nouvelle Lune ; Soleil 3 : premier quartier ; Soleil 4 : dernier quartier.

Action de la Lune :
On a deux marées par jour, chaque point de la Terre passant toutes les 12 heures sous un bourrelet (en réalité la direction Terre-Lune effectue un tour en une lunaison (28 jours) et on a un décalage de 24/28 h = 50’ entre deux marées consécutives).

Action du Soleil :
Lors de la pleine Lune (PL) et de la nouvelle Lune (NL), le Soleil accentue le bourrelet dû à la Lune : ce sont les marées de vives-eaux.

Lors des premier quartier (PQ) et dernier quartier (DQ), le Soleil et la Lune tendent à créer des bourrelets orthogonaux : ce sont les marées de mortes-eaux.

L’amplitude des marées oscille autour d’une valeur moyenne et a l’allure ci-dessous :

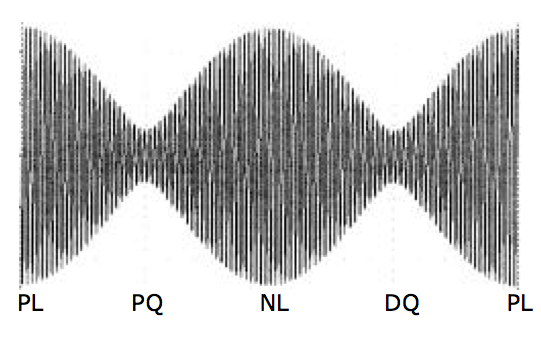
Amplitude des marées

En réalité :
c’est (un peu) plus compliqué et il faut tenir compte de phénomènes tels que les phénomènes de résonance, comme par exemple dans la baie du Mont Saint Michel.

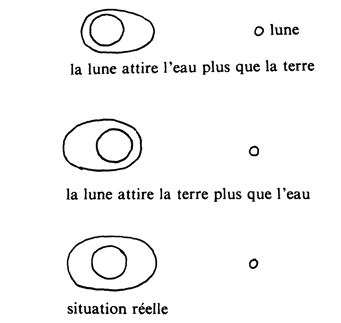
Richard Feynman, dans son livre « La nature de la physique » explique comment Newton résolut la difficulté qui restait dans la compréhension des marées, car « si la Lune attire les eaux, il ne devrait y avoir qu’une marée par jour, sous la Lune ... Newton fut en fait le premier à comprendre ce qui se passait :

la force que la Lune exerce sur la Terre et sur l’eau est la même pour une même distance, mais (voir la figure) l’eau est plus près de la Lune que la Terre solide sur la première vue, et plus loin sur la seconde. L’eau, sur la première vue, est attirée plus fortement vers la Lune que la Terre solide, et moins sur la seconde, de sorte que c’est une combinaison de ces deux schémas qui provoque la double marée ».

Marées selon Newton

3.2. Etude du terme centrifuge : la direction de la verticale

Dans ce qui suit on néglige le terme des marées dans le champ de pesanteur, alors (8) donne (9) :

$\vec{g} (M) = \vec{A_{Terre}} (M) + \vec{A_{astres}} (M) - \vec{A_{astres}} (O') + Ω^{2} \vec{HM}$ (8)

$\vec{P} (M) = m \vec{g} (M) = m \vec{g} (M) = m (\vec{A_{Terre}} (M) + Ω^{2} \vec{HM})$ (9)

Supposons la Terre à répartition sphérique de masse et M à la surface de la Terre et comparons la valeur du terme centrifuge maximal (à l’équateur) à celle du terme principal :

Direction de la verticale

$\vec{A_{Terre}} (M) = \frac{G M_{Terre}}{{R_{Tere}}^{2}} \vec{u_{MO'}}$ a pour valeur 9,83 $m . s^{- 2}$ et $\frac{Ω^{2} R_{Terre}}{A_{Terre}} = 3,4 . 10^{- 3} < < 1$ :

La direction de la verticale, définie par (9), passe pratiquement par le centre de la Terre et l’intensité du champ de pesanteur g(M) varie peu avec la latitude.

En tenant compte de l'aplatissement de la Terre aux pôles, dû aux forces centrifuges qui s'exercent sur le noyau fluide de la Terre : à l'équateur g est minimal et vaut $9,78 m . s^{- 2}$ ; aux pôles g est maximal et vaut $9,83 m . s^{- 2}$ . On peut prendre $g = 9,8 m . s^{- 2}$ à la surface de la Terre.

Si on néglige le terme centrifuge dans (9) : $\vec{P} (M) = m \vec{g} (M) = m \vec{g} (M) = m (\vec{A_{Terre}} (M) + Ω^{2} \vec{HM})$ , alors :

$\vec{P} (M)$ = m $\vec{g} (M) = m \vec{A_{Terre}} (M)$ et pour une Terre à répartition sphérique de masse : $\vec{g} (M) = \vec{g} (M_{0}) {(\frac{R_{Tere}}{R_{Terre} + h})}^{2}$ ,
h étant l'altitude du point $M$ , $M_{0}$ étant à l'aplomb de $M$ , au sol. ( $\vec{g} (M_{0})$ se note encore $\vec{g_{0}}$ ).

4. Influence du terme de Coriolis

Traitons l’exemple du sens des vents et courants marins à la surface de la Terre.

Considérons un point matériel M de masse m susceptible de se mouvoir sans frottement à la surface de la Terre, donc soumis à la réaction normale $\vec{R_{N}}$ .

D’après la figure suivante, avec $\vec{i}$ , $\vec{j}$ et $\vec{k}$ unitaires respectivement sur Ox, Oy et Oz :
$\vec{Ω} = - Ω \cos (λ) \vec{i} + Ω \sin (λ) \vec{k}$ .

Référentiel terrestre

D’après (7) : $m \vec{a_{T}} (M) = \vec{g} (M) + \vec{F_{ic}} + \vec{F_{appl}}$ , le principe fondamental de la dynamique appliqué dans le référentiel terrestre à ce point s'écrit :

$m \vec{a_{T}} (M) = m \vec{g_{0}} - 2 m \vec{Ω} \land \vec{v_{T}} (M) + \vec{R_{N}}$

M étant dans le plan horizontal : $\vec{OM} = x \vec{i} + y \vec{j}$ => ⇒ $\vec{v_{T}} (M) = \dot{x} \vec{i} + \dot{y} \vec{j}$ ⇒=> $\vec{a_{T}} (M) = \overset{..}{x} \vec{i} + \overset{..}{y} \vec{j}$

D’autre part, dans les simplifications précédentes : $\vec{g_{0}} = - g_{0} \vec{k}$ .

Avec finalement $\vec{R_{N}} = + R_{N} \vec{k}$ , le principe fondamental de la dynamique donne deux équations différentielles, dites couplées :

$\overset{..}{x} = + 2 Ω \sin (λ) \dot{y}$ et $\overset{..}{y} = - 2 Ω \sin (λ) \dot{x}$

La résolution peut se faire « à la main », ou par un logiciel de calcul formel comme Maple.

Pour un vent de vitesse $v = 10 m . s^{-}$ , selon Ox, au lieu O de latitude $∣ λ ∣ = 45^{°}$ , la solution est :

$x = \frac{1}{2} \frac{\sin (2 (\sin (λ) Ωt) v)}{Ω \sin (λ)}$ et $y = \frac{1}{2} \frac{[\cos (2 (\sin (λ) Ωt)) - 1] v}{Ω \sin (λ)}$

La trajectoire est un cercle de rayon $\frac{v}{2 Ω ∣ \sin (λ) ∣} = 97 km$ , parcouru à la vitesse v, dans le sens indirect dans l'hémisphère Nord $(λ = + 45^{°})$ , direct dans l'hémisphère Sud $(λ = - 45^{°})$ .

La force d’inertie de Coriolis est responsable d’autres phénomènes connus : déviation vers l’Est (dans les deux hémisphères) lors de la chute des corps, usure inégale des rails de chemin de fer, où elle intervient comme terme perturbateur.

Négliger l’influence du terme de Coriolis et ne prendre en compte que le terme principal dans le champ de pesanteur conduit, d’après (7), à l’écriture suivante du principe fondamental de la dynamique dans le référentiel terrestre :

$m \vec{a_{T}} (M) = m \vec{A_{Terre}} (M) + \vec{F_{ic}} + \vec{F_{appl}}$

Ceci revient à considérer le référentiel terrestre comme galiléen (sans terme d’inertie d’entraînement et sans force d’inertie de Coriolis).

5. Impesanteur

La propriété d’impesanteur provient du fait que le mouvement des corps soumis uniquement à l’interaction gravitationnelle est indépendant de leur masse. Elle ne s’observe en toute rigueur qu’au centre de masse d’un véhicule en mouvement sous l’action des seules forces gravitationnelles.

Soit un astronaute, dans une cabine spatiale, moteurs arrêtés, monté sur un pèse-personne.

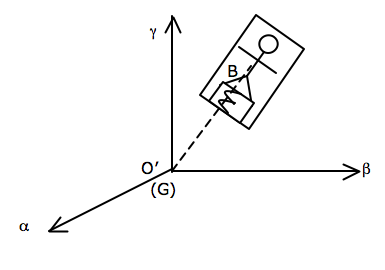
Impesanteur

Supposons le centre de masse B de l’astronaute, de masse m , confondu avec celui de l’ensemble cabine-contenu, de masse M .

Le référentiel géocentrique (G) est supposé ici galiléen.

Le principe fondamental de la dynamique appliqué à l’astronaute, considéré comme ponctuel, à l’équilibre dans le référentiel lié à la cabine, non galiléen, et soumis aux forces « véritables » : action gravitationnelle de la Terre (on néglige celle des autres astres) et tension du ressort, s’écrit :

$\vec{O} = m \vec{A_{Terre}} (B) + \vec{T} - m \vec{a_{e}} (B) - m \vec{a_{e}} (B)$ avec $\vec{a_{e}} (M) = \vec{a_{G}} (B)$ (point coïncidant) et $\vec{a_{c}} (M) = \vec{0}$ (équilibre relatif), on a :
$\vec{O} = m \vec{A_{Terre}} (B) + \vec{T} - m \vec{a_{G}} (B)$

Le principe fondamental de la dynamique appliqué à l’ensemble cabine-contenu, considéré comme ponctuel, dans le référentiel géocentrique galiléen, et soumis à l’action gravitationnelle de la Terre (on néglige celle des autres astres), s’écrit :

$M \vec{a_{G}} (B) = M \vec{A_{Terre}} (B)$ => $\vec{a_{G}} (B) = \vec{A_{Terre}} (B)$

Par comparaison des deux relations précédentes, on a : $\vec{T} = \vec{0}$ : c'est la propriété d'impesanteur.

Cet effet pourrait se ressentir dans un ascenseur en chute libre, ou dans un avion en chute libre : c’est dans un avion dont les moteurs compensent l’effet de la résistance de l’air, l’avion suivant alors la trajectoire parabolique d’une chute libre, que les astronautes sont entraînés à l'impesanteur (avion A300 zéro G).

Remarque.

Tout au long de ce chapitre, nous avons implicitement admis l’identité des masses inertielle et gravitationnelle. La propriété d’impesanteur en découle directement.

Rappelons que cette identité constitue le principe d’équivalence, à la base de la théorie de la relativité générale, et postulé par Einstein en 1916.