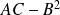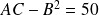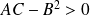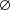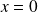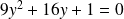Exo 17
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère le plan affine euclidien
de repère orthonormé
.
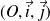Soit
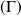la courbe d'équation :
.
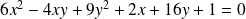Question
Question
Préciser les caractéristiques de la conique
.
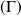Déterminez le repère
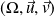et l'équation réduite.
Détermination du centre
Soit
.
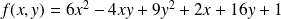Donc :
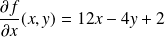, et :
.
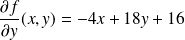Donc les coordonnées du centre
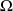de la conique sont solution du système :
.
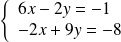Donc le centre de la conique est le point
.
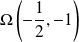Détermination du repère
La matrice
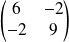a pour valeurs propres
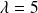et
.
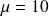Le sous-espace propre associé à
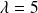est la droite d'équation :
.
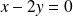Le sous-espace propre associé à
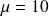est la droite d'équation :
.
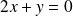Donc on pose :
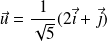, et :
.
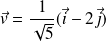Détermination de l'équation réduite
Soit
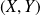les coordonnées du point
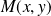dans le repère
.
Donc :
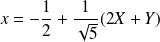, et :
.
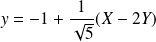En remplaçant dans l'équation de
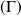, on obtient :
.
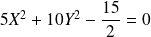Donc l'équation réduite de
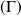dans
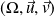est :
.
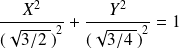Détermination des caractéristiques
Le demi-grand axe est
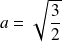et le demi-petit axe est
.
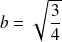Donc :
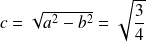, et :
.
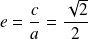On en déduit les coordonnées des sommets et des foyers, ainsi que les équations des axes et des directrices dans le repère
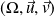, puis dans le repère
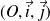à l'aide des formules de changement de repère :
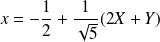et
.
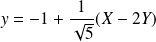Conclusion : La conique
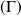est une ellipse de centre
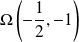et d'excentricité
.
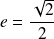Ses axes de symétrie ont pour équations :
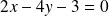et
.
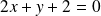Ses sommets sur le grand axe sont
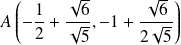et
.
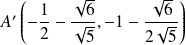Ses sommets sur le petit axe sont
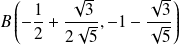et
.
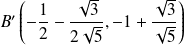Ses foyers sont
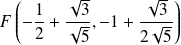et
.
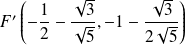Les directrices associées ont pour équations respectives :
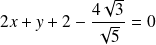, et :
.
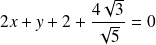Question
Construire la conique
.
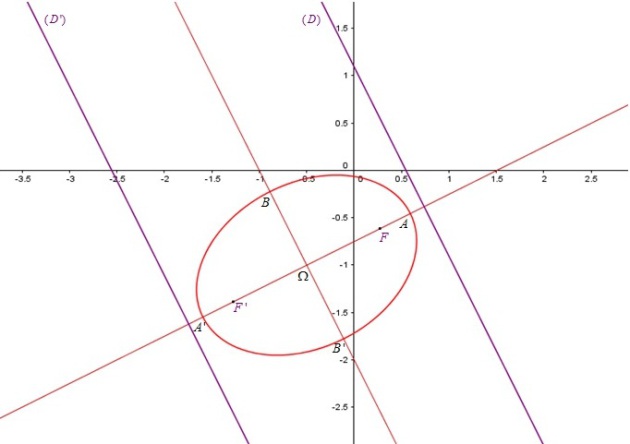
On peut remarquer que pour construire la courbe, il n'est pas nécessaire de calculer toutes les coordonnées : il suffit de tracer les axes de symétrie et de reporter les longueurs
,
,
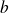et
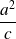sur les axes.
