Fonction dérivée
Définition :
Une fonction
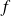 est dérivable sur un intervalle
est dérivable sur un intervalle
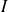 si la fonction
si la fonction
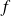 est dérivable en tout point de
est dérivable en tout point de
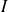 .
.
La fonction dérivée de
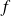 est la fonction
est la fonction
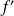 :
:
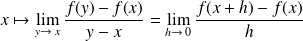 .
.
Le nombre dérivé de
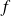 en
en
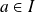 est donc
est donc
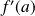 .
.
Une équation de la tangente à la courbe représentative de
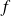 au point d'abscisse
au point d'abscisse
 est :
est :
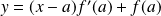 .
.
Les nombres dérivés à gauche et à droite de
 sont notés
sont notés
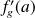 et
et
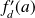 .
.
Fondamental :
Dérivées usuelles
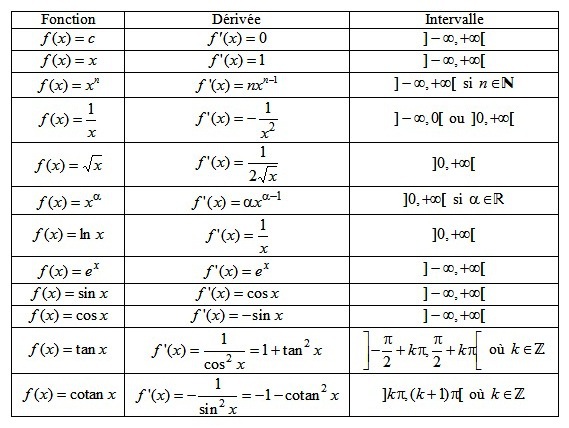
Fondamental :
Opérations algébriques
Soient
 et
et
 deux fonctions dérivables sur un intervalle
deux fonctions dérivables sur un intervalle
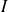 .
.
La fonction
 est dérivable sur
est dérivable sur
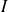 et
et
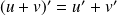 .
.Si
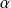 est une constante, la fonction
est une constante, la fonction
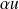 est dérivable sur
est dérivable sur
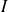 et
et
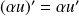 .
.La fonction
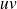 est dérivable sur
est dérivable sur
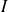 et
et
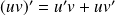 .
.Si la fonction
 ne s'annule pas, la fonction
ne s'annule pas, la fonction
 est dérivable sur
est dérivable sur
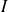 et
et
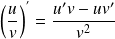 .
.
Les deux premières propriétés montrent que l'application
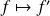 est linéaire.
est linéaire.
Si la fonction
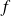 est à valeurs complexes :
est à valeurs complexes :
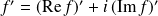 .
.
Fondamental :
Composition
Si la fonction
 est dérivable sur un intervalle
est dérivable sur un intervalle
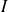 et si la fonction
et si la fonction
 est dérivable sur l'intervalle
est dérivable sur l'intervalle
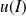 , alors la fonction
, alors la fonction
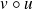 est dérivable sur
est dérivable sur
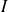 et
et
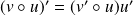 .
.
Conséquences
Si
 est une fonction dérivable :
est une fonction dérivable :

Fondamental :
Fonction réciproque
Si la fonction
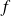 est dérivable sur un intervalle
est dérivable sur un intervalle
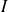 , si
, si
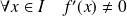 et si
et si
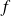 est bijective de
est bijective de
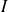 dans
dans
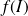 , alors sa réciproque
, alors sa réciproque
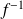 est dérivable sur
est dérivable sur
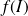 et
et
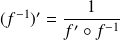 .
.
Fondamental :
Conséquences
La fonction Arccosinus est dérivable sur
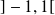 et
et
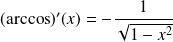 .
.La fonction Arcsinus est dérivable sur
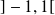 et
et
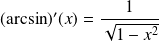 .
.La fonction Arctangente est dérivable sur
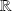 et
et
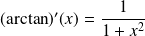 .
.





