Exo 18
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
une suite strictement positive.
On considère la suite
définie par
et par la relation :
.
Question
Montrer que la suite
est bornée si et seulement si la suite
est bornée.
Démontrez successivement les deux implications.
Si
est bornée, exprimez
en fonction de
et
pour montrer que
est bornée.Si
est bornée, cherchez une condition suffisante pour qu'un réel
soit (par récurrence) un majorant de la suite
.
On démontre successivement les deux implications.
On suppose que la suite
est bornée.Or :
. Donc la suite
est bornée.
On suppose que la suite
est bornée.Donc :
.Pour montrer que la suite
est bornée, il faut trouver un réel
tel que :
. Donc il faut déjà que :
.Il faut ensuite que, si
, alors
. Pour cela, il suffit que
vérifie l'inégalité :
, donc
.Soit
la fonction définie sur
par :
. Donc
.Donc
est décroissante sur
et croissante sur
.Or
et
. Donc :
.La fonction
est continue et strictement croissante sur
, donc définit une bijection de
dans
. Donc l'équation
admet une unique solution
dans
, et :
.Donc pour que
, il suffit que :
, donc que :
.Donc si
, on a
et si
, alors
.Donc par récurrence :
. Donc la suite
est bornée.
Conclusion : La suite
est bornée si et seulement si la suite
est bornée.
Question
Montrer que la suite
est convergente si et seulement si la suite
est convergente.
Démontrez successivement les deux implications.
Si
est convergente, exprimez
en fonction de
et
pour montrer que
est convergente.Si
est convergente, déterminez la seule limite possible
de la suite
, puis démontrez que
tend vers
.
On démontre successivement les deux implications.
On suppose que la suite
est convergente. Soit :
, donc :
.Or :
. Donc la suite
est convergente vers :
.
On suppose que la suite
est convergente. Soit :
, donc :
.D'après ce qui précède, si la suite
converge, sa limite vérifie :
.L'étude de la fonction
est similaire à celle de la fonction
étudiée dans la question précédente. Donc il existe un unique réel
qui annule la fonction. Donc :
et
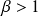.Montrons que la suite
converge vers :
(donc
).On a :
. Donc :
.Donc :
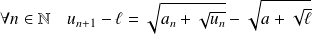.Donc :
. Et :
.Donc :
.Or :
. Donc :
.Donc :
.Donc :
.Donc par récurrence :
.Donc :
.Soit
. Le réel
était quelconque, donc on choisit
, ce qui détermine l'entier
. Donc :
.Si
, alors :
.
Si
:
car
puisque
.Donc :
.
Donc dans les deux cas :
.Donc la suite
converge vers
.
Conclusion : La suite
est convergente si et seulement si la suite
est convergente.
