Polynômes d'endomorphismes
Dans ce qui suit,
désigne un espace vectoriel.
Définition :
Si
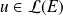et si
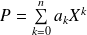, on leur associe l'endomorphisme :
.
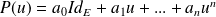Théorème de décomposition des noyaux :
Si
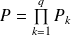, où
, ...,
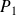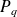sont des polynômes
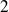à
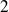premiers entre eux, alors :
.
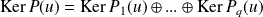Définition :
Un polynôme
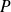est un polynôme annulateur d'un endomorphisme
si
.
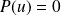L'ensemble des polynômes annulateurs de
est un idéal de
.
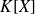S'il n'est pas réduit à
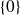, il est engendré par un unique polynôme unitaire
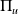appelé polynôme minimal de
.
En dimension finie, tout endomorphisme a un polynôme minimal.
Définition :
Un sous-espace vectoriel
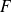de
est stable par un endomorphisme
si
.
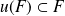Fondamental :
Propriétés :
Si
et
sont des endomorphismes qui commutent (
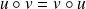), alors
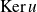et
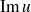sont stables par
.Si
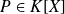, le noyau et l'image de
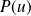sont stables par
.Si
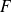est un sous-espace vectoriel stable par
et
, alors
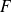est stable par
, par
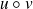, et par tout polynôme
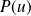.Si
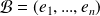est une base de
« adaptée » à un sous-espace
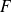, c'est-à-dire telle que
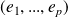soit une base de
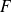, le sous-espace
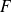est stable par un endomorphisme
si et seulement si la matrice de
dans
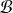est de la forme
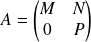, où
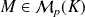est la matrice de la restriction de
à
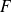. Alors :
.
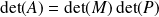