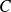Ensemble des nombres complexes

Exo 12

Commencez par chercher à résoudre l'exercice par vous-même.

Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.

Une solution détaillée vous est ensuite proposée.

Soit triangle de sens direct.

On construit les triangles , et équilatéraux directs.

Soient , et les centres de gravité respectifs des triangles , et .

Question

Démontrer que le triangle est équilatéral de même centre de gravité que le triangle .

Indice

Démontrez que le point est l'image du point par la rotation de centre et d'angle .

Solution

Soient , et les affixes des points , et dans un repère orthonormal direct.

Le triangle est équilatéral direct.

Donc le point est l'image du point par la rotation de centre et d'angle .

Donc son affixe vérifie : en posant : .

Donc le point a pour affixe : .

Le centre de gravité du triangle a pour affixe .

Donc le point a pour affixe : .

De même le triangle est équilatéral direct.

Les calculs sont analogues en remplaçant par , et par .

Donc son centre de gravité a pour affixe : .

De même le triangle est équilatéral direct.

Les calculs sont analogues en remplaçant par , et par .

Donc son centre de gravité a pour affixe : .

On peut déjà voir que :

.

Donc le centre de gravité du triangle a pour affixe .

Conclusion : Les triangles et ont même centre de gravité .

D'autre part :

.

Et : .

Donc : .

Or . Donc : .

Donc : . Donc : .

Donc le point est l'image du point par la rotation de centre et d'angle .

Conclusion : Le triangle est équilatéral.

PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimer Paternité - Pas d'Utilisation Commerciale - Partage des Conditions Initiales à l'IdentiqueRéalisé avec Scenari (nouvelle fenêtre)