Enoncé
6) On considère un nombre réel ![]() . Soit
. Soit
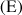 l'équation
l'équation ![]() , d'inconnue complexe
, d'inconnue complexe
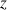 . Pour tout
. Pour tout ![]() , l'équation
, l'équation
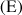 a deux solutions réelles.
a deux solutions réelles.
Résultat
Correction
Explications
En effet, l'équation
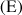 :
: ![]() a pour discriminant :
a pour discriminant :
Lorsque ![]() ,
, ![]() n'est pas toujours positif, donc
n'est pas toujours positif, donc
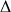 n'est pas toujours positif.
n'est pas toujours positif.
L'équation
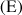 n'a donc pas toujours deux solutions réelles (en prenant par exemple
n'a donc pas toujours deux solutions réelles (en prenant par exemple ![]() , on trouve deux solutions complexes non réelles).
, on trouve deux solutions complexes non réelles).