On va maintenant généraliser à une intégrale sur un domaine quelconque ce qui a été vu sur une intégrale sur un parallélépipède rectangle.

Lorsque le domaine 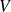de l'espace n'est pas un parallélépipède rectangle on peut refaire le raisonnement du paragraphe référencé et ramener le calcul de l'intégrale triple à celui d'une intégrale simple et d'une intégrale double. La difficulté consiste à trouver les "bonnes" bornes de cette intégrale simple et de cette intégrale double.

On suppose que le domaine 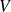peut être défini par :

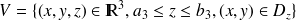
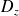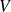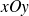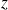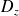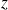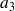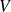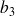où est le domaine (plan) intersection du volume avec le plan parallèle à qui a pour cote , ce domaine varie avec en général. est la plus petite cote des points du domaine et la plus grande cote des points de 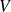comme le montre la figure "Bornes de l'intégrale triple".

On peut montrer que

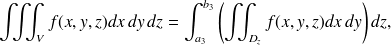
Une manière imagée d'expliquer cette première méthode est de dire que l'on découpe le domaine en "tranches" (penser à un saucisson ! ) et on parlera alors de la méthode de calcul par tranches de l'intégrale triple.

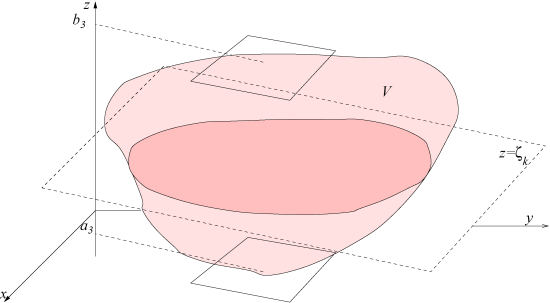
Dans la formule précédente on a privilégié l'axe Oz. On aurait pu aussi bien privilégier l'axe Oy, ce qui donnerait

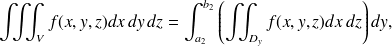
où 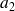est la plus petite ordonnée des points du domaine 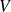et 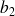la plus grande ordonnée des points de 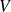, et le domaine plan 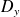est l'intersection de 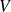avec le plan parallèle au plan 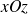et d'ordonnée .

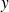On obtient une formule similaire en privilégiant .

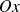Dans la méthode des tranches, on a exprimé une intégrale triple 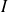comme une intégrale simple d'intégrale double, on peut également exprimer 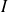comme une intégrale double d'intégrale simple, c'est la méthode des bâtons qui va être décrite dans le paragraphe suivant.