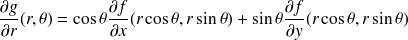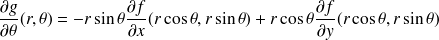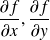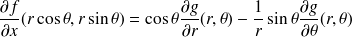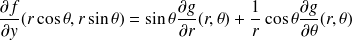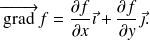Le plan est muni d'un repère orthonormé .

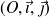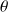Si et sont les coordonnées polaires d'un point 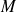de 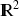, différent de 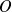, on définit les vecteurs

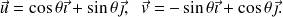
Si f est une fonction de 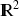dans 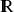, différentiable en 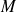, on définit la fonction 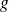par 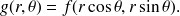Montrer que le gradient s'écrit :

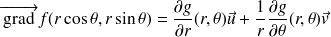
Pour ce faire on pourra utiliser les règles de dérivation des fonctions composées pour calculer les dérivées partielles de 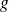en fonction des dérivées partielles de 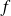, puis en déduire les dérivées partielles de 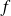en fonction de celles de 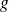et enfin remplacer dans l'expression du gradient.