La règle à calcul
Entrez des nombres dans les champs jaunes et cliquez sur "Calculer".
Le principe de la règle à calcul est l'isomorphisme entre les groupes
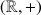et
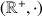. Ainsi, la multiplication dans
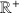est transformée en addition de deux nombres positifs, ce qui se fait très bien mécaniquement à l'aide de réglettes.
L'isomorphisme qui est utile ici s'écrit
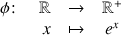
avec
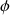la fonction réciproque du logarithme :
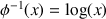. On obtient :
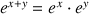ou bien encore
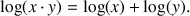
Si bien que
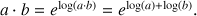
Le calcul de
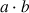à l'aide de la règle à calcul fait intervenir les deux termes par leur logarithme, qu'on additionne ensuite, et on transforme ce résultat de nouveau par l'exponentielle.
Cette transformation de va et vient par l'exponentielle et le logarithme se fait très simplement par une graduation logarithmique et non pas linéaire sur la règle.
Supposons que vous vouliez calculer
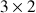. Alignez la graduation 1 de la réglette avec le chiffre 3 de la règle. Puis faites glisser jusqu'à la graduation 2 de la réglette le curseur mobile. Vous lisez le résultat sur la graduation fixe de la règle (ici, 6).
Quand le résultat est en dehors de la règle, il faut procéder différemment. Explorez donc avec l'appliquette.
