Réponse impulsionnelle
Le système causal, linéaire et invariant est entièrement décrit par sa réponse impulsionnelle : c'est le signal noté
, réponse du système à l'entrée, impulsion de Dirac 
. On peut en parler comme de la « signature » du système.
Exemple :
On peut rendre cette notion théorique sensible par l'exemple suivant : la réponse impulsionnelle d'une salle de concert ou d'une église est approchée qualitativement par la manipulation simple suivante : vous frappez sèchement dans vos mains (approximation d'un Dirac) et vous entendez pendant quelques secondes (surtout s'il y a de la réverbération) une approximation de la réponse impulsionnelle.
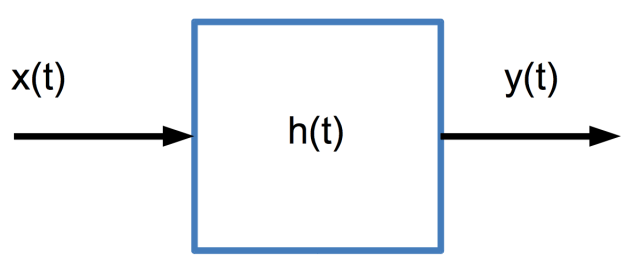
Le concept est généralement illustré par le schéma « boîte noire » avec 
comme entrée et 
en sortie, suivant que nous utiliserons régulièrement :
On fait figurer la réponse impulsionnelle dans la boîte puisqu'elle décrit entièrement la système. On parle de "boîte noire" en ce sens qu'on n'a pas besoin d'en connaître la structure intime, c'est-à-dire les composants qui la définissent. A la limite, si on est capable de déterminer cette réponse impulsionnelle expérimentalement (comme dans l'exemple de la salle de concert ci-dessus), il n'est alors pas nécessaire d'écrire les équations de la physique (généralement des équations différentielles) qui régissent le système.
Nous formulons à présent en termes mathématiques les hypothèses de causalité, linéarité et invariance puis nous montrons comment cela permet d'écrire la réponse du système à une entrée quelconque moyennant un concept inédit, le produit de convolution.
Le système est causal : cela signifie que la sortie ne peut précéder l'entrée : ainsi, l'impulsion de Dirac, 
correspondant à l'entrée non nulle en t=0, la réponse impulsionnelle est nécessairement nulle pour t négatif.
Le système est linéaire : si le système répond à 
par 
et à 
par 
alors, il répond à 
par 
où 
et
sont deux scalaires complexes .
Le système est invariant : si le système répond à 
par 
alors il répond à 
par 
.
